1.Область определения - вся числовая ось ( нет особых точек).
2. Ф-я не четная и не нечетная т.к. f(x) !=f(-x) и f(x) != -f(x)
3. Ф-я непереодическая
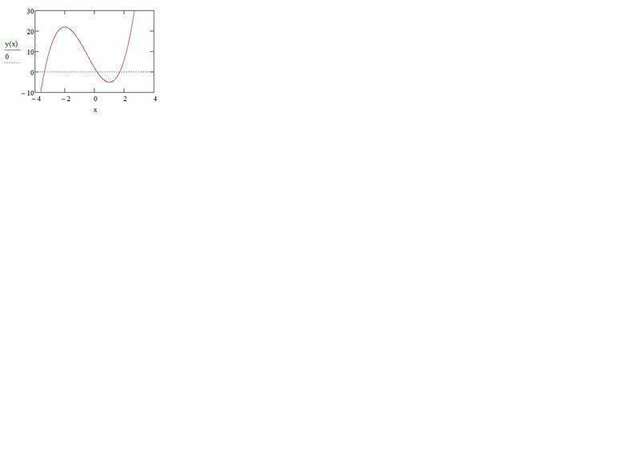
4. Найдем корни - это точки пересечения с осью Х (-3,369; 0,175; 1,694)
(примечание: корни могут быть найдены только численными методами, аналитического выражения нет). y(0)=2 (пересечение с осью У)
5. Для нахождения точек экстремума берем 1-ю и 2-ю производные, приравниваем их 0. По 1-й производной 6x^2+6x-12 (корни = 1; -2) Экстремумы в точках: 1;-2.
Так как 2-я производная (12х+6) в (.)-2 отрицательна, то в (.) -2 имеем максимум,
так как 2-я производная в (.) 1 положительна. то в (.) 1 имеем минимум.
Приравняв 0 2-ю производную, получаем точку перегиба = (-0.5).
Итак, функция возрастает на интервале (-беск,-2), убывает в интервале (-2,1) и возрастает в интервале (1,+беск).