1. Область определения функции: множество всех действительных чисел.
D(y)=R
2. Функция не периодическая
3. y(-x)=-2x³-x^4=-(2x³+x^4)
Итак, функция ни четная ни нечетная.
4. Точки пересечения с осью Оу и Ох
4.1. С осью Ох(у=0)

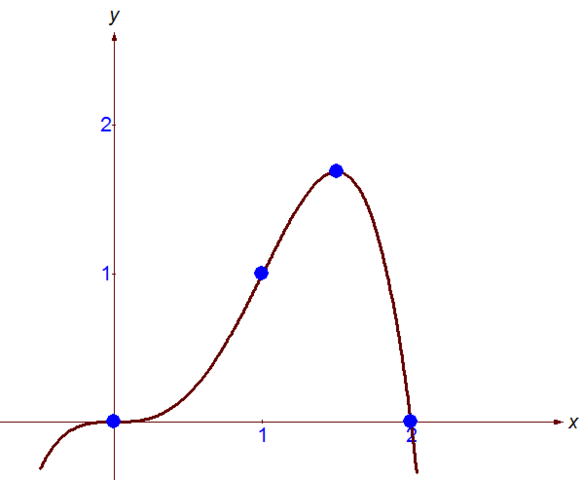
(0;0), (2;0) - точки пересечения с осью Ох
4.2. С осью Оу (х=0)
у=0
(0;0) - точки пересечения с осью Оу
5. Критические точки(возрастание и убывание функции)

___-__(0)___+____(1.5)____-___
Итак, функция возрастает на промежутке x ∈ (0;1.5), а убывает на промежутке x ∈ (-∞;0) и x ∈ (1.5;+∞). В точке х=0 функция имеет локальный минимум, а в точке х=1,5 - локальный максимум
6. Точки перегиба

___-__(0)___+___(1)__-___
Функция выпукла на промежутке x ∈ (-∞;0) и x ∈ (1;+∞), а вогнута на промежутке х ∈ (0;1)
Вертикальных, гортзонтальных и наклонных асимптот нет