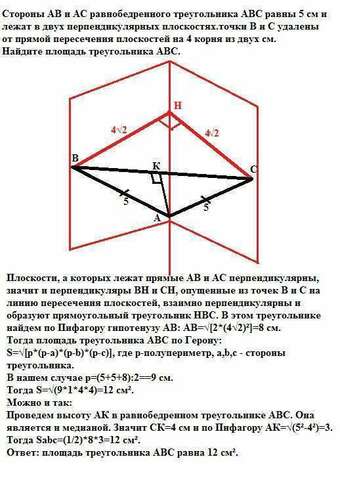
Плоскости, а которых лежат прямые АВ и АС перпендикулярны, значит и перпендикуляры ВН и СН, опущенные из точек В и С на линию пересечения плоскостей, взаимно перпендикулярны и образуют прямоугольный треугольник НВС.
В этом треугольнике найдем по Пифагору гипотенузу ВС:
ВС=√[2*(4√2)²]=8 см.
Тогда площадь треугольника АВС по Герону:
S=√[p*(p-a)*(p-b)*(p-c)], где р-полупериметр, a,b,c - стороны треугольника.
В нашем случае р=(5+5+8):2==9 см.
Тогда S=√(9*1*4*4)=12 cм².
Можно и так:
Проведем высоту АК в равнобедренном треугольнике АВС. Она является и медианой.
Значит СК=4 см и по Пифагору АК=√(5²-4²)=3. Тогда Sabc=(1/2)*8*3=12 cм².
Ответ: площадь треугольника АВС равна 12 см².