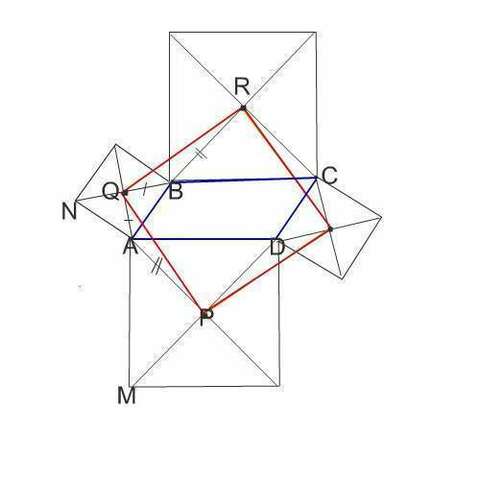
Сделаем рисунок.
Обозначим буквами P, Q и Rцентры квадратов, построенных на сторонах DA, AB и BC параллелограмма.
Острый угол при вершине A обозначим α.
∠ PAQ = 1/2∠DAM +1/2∠BAN+ α = 90º+α
∠ RBQ=360º-(180º-α) - 90º=180º- 90º+α=90º+α .
∠ PAQ =∠ RBQ
QB=AQ, BR=AP как половины равных диагоналей, а значит,
Δ PAQ = Δ RBQ.
PQ=RQ.
Стороны AQ и BQ этих треугольников перпендикулярны, поэтому PQ ⊥ QR.
Так же доказывается перпендикулярность других углов четырехугольника с равными сторонами.
Центры построенных на сторонах параллелограмма квадратов являются вершинами квадрата.