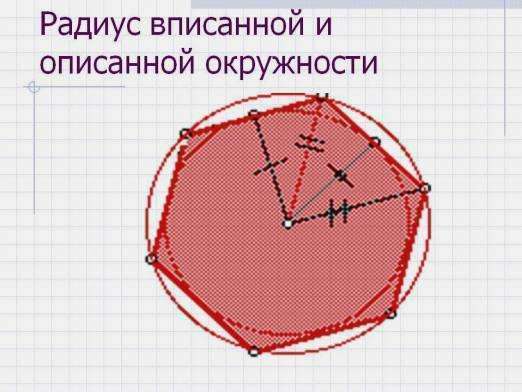
Радиус описанной окружности правильного многоугольникаПравильный многоугольник - это такой многоугольник, у которого равные стороны и углы. А угол между соседними вершинами правильного n-угольника равен:BOA = x = 360°/n, где BOA - треугольник, x - длина его основания, n - это число сторон правильного многоугольника.Построим треугольник BOA отдельно. О нём нам известно:он равнобедренный;бедра треугольника BOA - это так же радиусы описанной окружности правильного n-угольника;длина основания «x» треугольника BOA - это сторона исходного правильного многоугольника.угол между радиусами R, который мы прежде вычислили по формуле (**).В первую очередь необходимо опустить высоту на основание и рассмотреть прямоугольный треугольник, который у нас получился. С помощью тригонометрических функций угла (в данном случае острого) получаем:sin(360°/2n) = x/2R, с чего получаем формулу собственно радиуса описанной окружности правильного n-угольника:R = x/(2sin(360°2n)), R - это радиус описанной окружности правильного n-угольника, x - сторона правильного многоугольника и n - это число сторон правильного многоугольника.