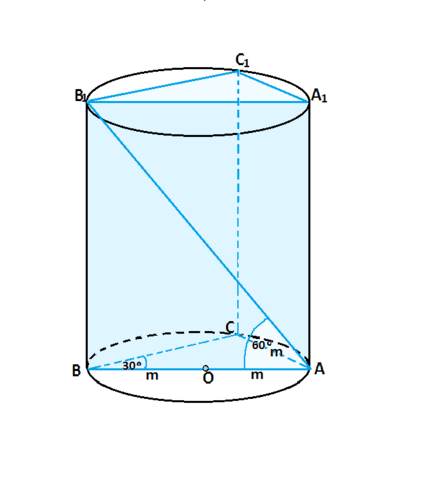
В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен m,а противолежащий угол равен 30°. Диагональ большей боковой грани призмы наклонена к плоскости ее основания под углом 60 °. Найдите объем цилиндра и его площадь и площадь боковой поверхности
Пусть центр нижнего основания цилиндра будет О, а основание вписанной призмы -
⊿ АВС, где ∠С=90° а ∠В=30°
Так как катет АС, равный
m, противолежит углу 30°, гипотенуза
АВ =АС:sin(30°)=2m
Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы. Следовательно,
ВО=ОА=
R=m.
Объем цилиндра
V=S*H
Сумма острых углов прямоугольного треугольника равна 90°
Треугольник АВВ1 - прямоугольный с острым углом ВАВ1=60°
H=ВВ1=AB*tg (60°)=2m*√3
V=π*m²*2m*√3=2π m³√3
Площадь боковой поверхности
S=L*H=2πr*H=2πm*2m*√3=4πm²*√3