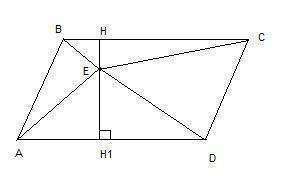
Построим высоту НН1, проходящую через точку Е. Найдем площадь треугольника ВЕС (обозначим ее за S1):
S1=1/2BC*EH (отрезок ЕН будет являться высотой треуг-ка ВЕС).
Найдем площадь треугольника AED (обозначим ее за S2):
S2=1/2AD*EH1 (отрезок ЕН1 - высота треуг-ка АЕD).
S1+S2=1/2BC*EH+1/2AD*EH1=1/2(BC*EH+AD*EH1). Учитывая, что в параллелограмме ВС=AD, можно записать:
S1+S2=1/2(AD*EH+AD*EH1)=1/2AD(EH+EH1).
Площадь параллелограмма S равна:
S=AD*HH1.
НН1=ЕН+ЕН1. Тогда
S1+S2=1/2AD*HH1. Таким образом
S1+S2=1/2S