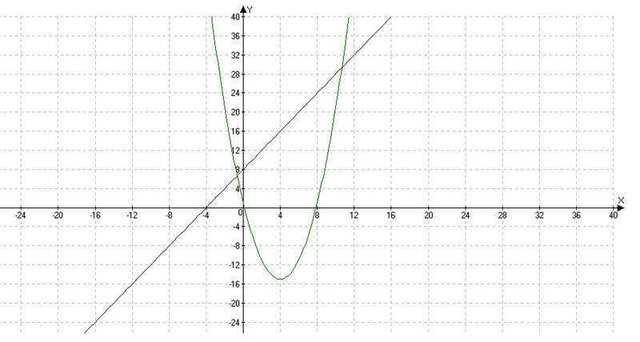
Найдём корни параболы:
D^2=16-1=15;
x_1,2=4±√15;
прямая пересекает ох в точке с абциссой -4
прямая и парабола пересекаются в двух точках. Решив систему данных уравнений, найдём в каких:
y = 2x + 8
x^2 – 8x + 1=2x+8; <=> x^2 – 10x - 9 = 0 <=> x=5±√34
Теперь возьмём интеграллы:
S=A-B-C-D;




Дальше - алгебра.