Теорема
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне S = a * h.
Доказательство
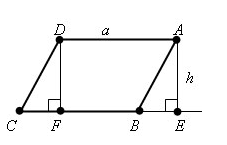
Пусть ABCD – данный параллелограмм. Если он не является прямоугольником, то один из его углов A или B острый. Пусть A острый.
Опустим перпендикуляр AE из вершины A на прямую CB. Площадь трапеции AECD равна сумме площадей параллелограмма ABCD и треугольника AEB. Опустим перпендикуляр DF из вершины D на прямую CD. Тогда площадь трапеции AECD равна сумме площадей прямоугольника AEFD и треугольника DFC. Прямоугольные треугольники AEB и DFC равны, а значит, имеют равные площади. Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника AEFD, т.е. равна AE * AD. Отрезок AE – высота параллелограмма, соответствующая стороне AD, и, следовательно, S = a * h. Теорема доказана.