** сторонах АС и ВС треугольника АВС вне треугольника построены квадраты ACDE и BFKC....

Question

На сторонах АС и ВС треугольника АВС вне треугольника построены квадраты ACDE и BFKC. Точка М – середина стороны.
а) Докажите, что СМ =1/2DK.
б) Найдите расстояние от точки М до центров квадратов, если АС=6, ВС=10 и угол АСВ равен 30°.

Answer 1

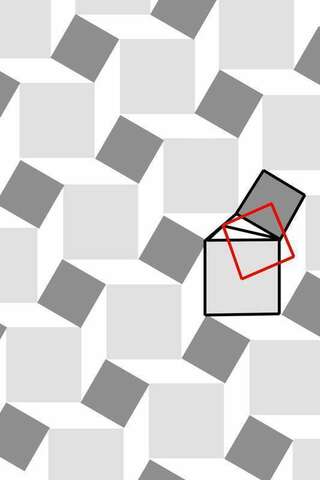
Вся эта конструкция является частью замощения плоскости, представленного на рисунке.
Замощение переходит "в себя" при повороте всей плоскости на 90° вокруг центра любого из квадратов.
Все "белые" параллелограммы равны между собой. Отсюда следует а).
б) Фигура, изображенная красным на рисунке - это квадрат. Поскольку, к примеру, две её стороны, выходящие из центра большего квадрата, равны и перпендикулярны (еще раз - одна переходит в другую при повороте на 90° вокруг их общей вершины). То же касается и двух сторон, у которых общая вершина - центр меньшего квадрата.
Поэтому расстояние от M до центров квадратов одинаковое, и равно стороне красного квадрата. Проще всего найти диагональ этого квадрата - надо соединить центры большого и малого квадратов с точкой C и между собой. Получится треугольник O1O2C с углом O1CO2;
∠O1CO2 = ∠ACB + ∠O1CA + ∠O2CB = 30° + 45° + 45° = 120°; и сторонами AO1 = 6√2/2 = 3√2; BO2 = 10√2/2 = 5√2;
Отсюда (O1O2)^2 = (5√2)^2 + (3√2)^2 + 2*(5√2)*(3√2)*(1/2) = 2*49;
O1O2 = 7√2; откуда MO1 = MO2 = 7;

---

Comments

конечно, задача элементарно решается с помощью векторов - надо ввести две пары взаимно перпендикулярных единичных векторов, так, чтобы одна пара переходила в другую при повороте на 120° к примеру CD = a*i; CA = a*j; CB = -b*m; CK = b*n; i^2 = j^2 = m^2 = n^2 = 1; тогда KD = a*i - b*n; CM = (a*j - b*m)/2; поскольку in = jm; а) доказано

---

кстати, 120° - это я уже использовал значение угла С, в общем случае С + 90°; для б) легко найти MO2 = CO2 - CM = b*(n - m)/2 - (a*j - b*m)/2 = (b*n - a*j)/2; (nj = - 1/2; если угол С = 30°; косинус угла 120°); отсюда получается ответ, и НЕЗАВИСИМО легко найти также MO1;

---

Спасибо) через векторы действительно проще...

---

Выложенное решение само по себе важное - оно показывает связь таких построений со скрытыми инвариантами. В данном случае есть инвариантность относительно сдвигов и относительно поворотов, и этого достаточно, чтобы решить задачу без всяких формул. Ответ является следствием глубокой симметрии, которая присутствует в задаче, но как-бы скрыто, незаметно.

---

А как вы так сразу определили, что эта пространственная структура должна выглядеть именно так, или вы взяли одну инвариантность из многих?

---

сразу определил :) но я знал, что искать :)

---

вы же наверно понимаете, что это не я открыл :) есть целые разделы геометрии, которые занимаются периодическими конструкциями. Замощения плоскости - одна из известных штук.