Стороны прямоугольника равны 9 и 12 см. Из середины большей стороны восстановлен...

Question

Стороны прямоугольника равны 9 и 12 см. Из середины большей стороны восстановлен перпендикуляр длиной 4,8см к плоскости прямоугольника. Найти расстояние от конца этого перпендикуляра до одной из диагоналей.
Приложите , пожалуйста, рисунок для решения.

Answer 1

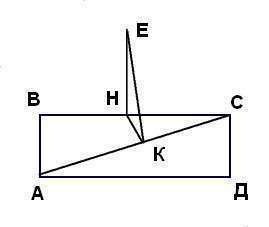
Прямоугольник АВСД (АВ=СД=9 и ВС=АД=12)
Середина большей стороны - точка Н: (ВН=НС=ВС/2=6)
Перпендикуляр ЕН=4,8
Нужно найти расстояние ЕК до диагонали АС.
Диагональ АС=√(АВ²+ВС²)=√81+144=√225=15
Прямоугольные ΔСКН (Значит НК/СД=НС/АС
НК=СД*НС/АС=9*6/15=3,6
Из прямоугольного ΔЕНК 
ЕК=√(ЕН²+НК²)=√(23,04+12,96)=√36=6

---