Помогите пожалуйста Радиус основания равностороннего цилиндра равен 12 см; точка...

Question

Помогите пожалуйста
Радиус основания равностороннего цилиндра равен 12 см; точка пересечения диагоналей его осевого сечения является центром сферы радиуса 15 см. Найдите площадь части сферической поверхности, находящейся вне цилиндра.

Answer 1

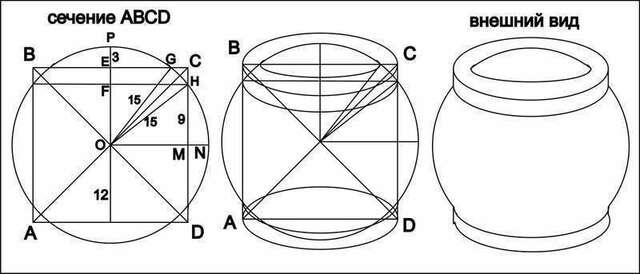
OM=OF=12
OP=15, PE=3
OM=12, по теореме Пифагора HM=9=FO
PF=15-FO=6

S шара (площадь поверхности)= 4пR^2
S сегмента =2пRH 
где Н - высота сегмента
S сегмента с высотой РЕ = 2пR*3=90п
S сегмента с высотой PF=2пR*6=180п
S поверхности вне цилиндра = S шара + 2(S сегмента с высотой РЕ) - 2(S сегмента с высотой PF) =900п-360н+180п=720п

Ответ:720п

---

Comments

сможете?

---

да

---

спасибо большое ))))

---

ну что , получилось

---

ответ есть?

---

да,18п

---

также получилось, щас решение напишу

---

хорошо, спасибо

---

я тебе решение напишу в вопрос, а не в комментарий, чтоб картинку вставить

---

хорошо)