Неравенство:
(a-3)x^2 - (a+1)x + (a+1) >= 0
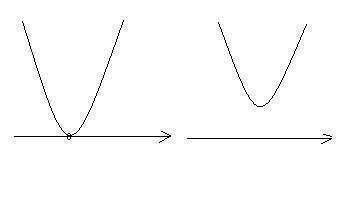
В общем, нужно понять, что если ветви параболы направлены
вверх и неравенство f(x) >= 0 выполняется при любом х, то
возможны два случая, нарисованные на картинке:
Или вершина касается оси Ох (D = 0), или находится выше (D < 0).
1) Вершина параболы находится на оси Ox и D = 0.
D = (a+1)^2 - 4(a-3)(a+1) = (a+1)(a+1 - 4(a-3)) = (a+1)(13-3a) = 0
a1 = -1, a2 = 13/3
2) Вершина находится выше оси Ox и D < 0
D = (a+1)^2 - 4(a-3)(a+1) = (a+1)(a+1 - 4(a-3)) = (a+1)(13-3a) < 0
a < -1 U a > 13/3
По факту можно было решить одно неравенство
D = (a+1)^2 - 4(a-3)(a+1) = (a+1)(a+1 - 4(a-3)) = (a+1)(13-3a) <= 0<br>a <= -1 U a >= 13/3
Но еще нужно учесть вот какой момент.
Если член x^2 = 0, то парабола вырождается в прямую, и она уже не будет положительна при любых х. То есть при каком-то х она пересечет ось Ох и станет отрицательной.
Поэтому a =/= 3 = 9/3 < 13/3.
Но нам повезло, число 3 и так не входит в ответ.
Ответ: a принадлежит (-oo; -1] U [13/3; +oo)