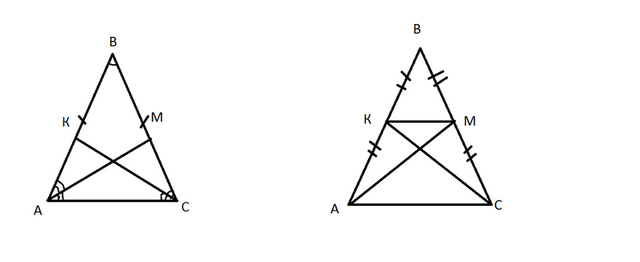
А) рассмотрим ΔАВМ и ΔСКВ (рис.1) КС и АМ -биссектрисы
угол В-общий,( АВ=ВС, уголА=уголС)-так как ΔАВС-равнобедренный, угол ВАМ=угол КСВ= 0,5 угла А=0,5 угла С ⇒ΔВАМ=ΔВКС - по второму признаку ⇒АМ=КС
б) рассмотрим ΔАКМ и ΔСКМ (рис.2) ,АМ и СК-медианы, т.к. АВ=ВС,то ВМ=МС= ВК=АК (по свойсву медиан) ⇒ КМ-средняя линия ΔАВС ⇒АС || КМ ⇒АКМС-равнобедренная трапеция и угол АКМ=угол КМС, КМ-общая сторона;
если угол АКМ=угол КМС, КМ-общая сторона, АК=МС, то ΔАКМ=ΔКМС - по 1 признаку ⇒АМ=СК