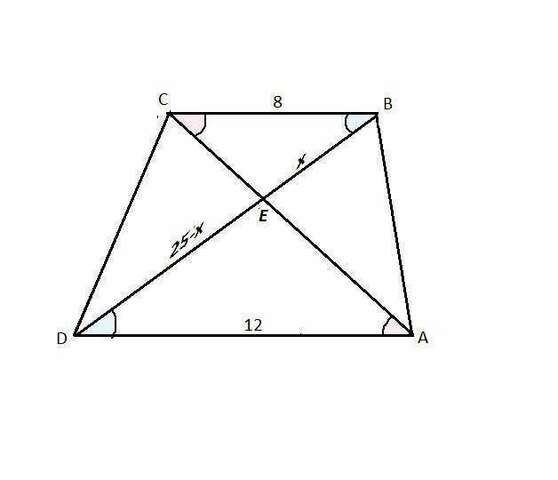
Диагонали трапеции делят ее на 4 треугольника, причем треугольники, примыкающие к боковым сторонам, равновелики, а к основаниям - подобны. т.к. соответственные углы в них - равные накрестлежащие при параллельных основаниях и секущих- диагоналях.
Итак, треугольники ВСЕ и АЕD - подобны.
Пусть ВЕ=х, тогда ЕD= 25-x.
Из подобия треугольников:
ВС:АD=BE:ED
8:12=x:(25-х)
12х=200-8х
20х=200
х=10
ВЕ=10 см