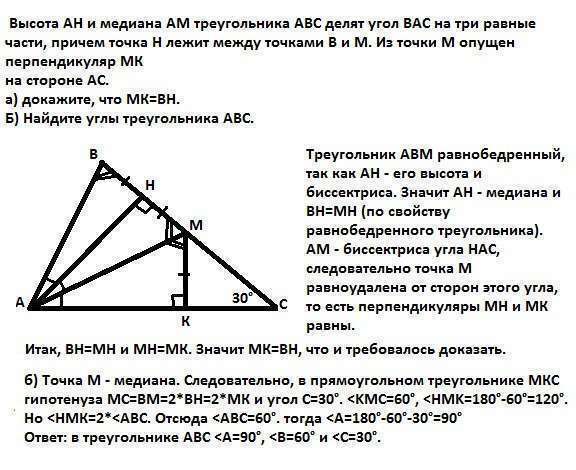
Треугольник АВМ равнобедренный, так как АН - его высота и биссектриса. Значит АН - медиана и ВН=МН (по свойству равнобедренного треугольника).
АМ - биссектриса угла НАС, следовательно точка М равноудалена от сторон этого угла, то есть перпендикуляры МН и МК равны.
Итак, ВН=МН и МН=МК. Значит МК=ВН, что и требовалось доказать.
б) Точка М - медиана. Следовательно, в прямоугольном треугольнике МКС гипотенуза МС=ВМ=2*ВН=2*МК и угол С=30°. Ответ: в треугольнике АВС