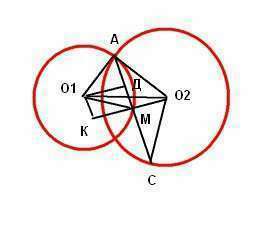
А) Радиусы окружности с центром О₁ О₁А=О₁В=О₁М.
Радиусы окружности с центром О₂ О₂А=О₂В=О₂С
Из О₁ на АС опустим перпендикуляр О₁Д..
Из О₂ на АС перпендикуляром будет О₂М, т.к. точка М делит хорду пополам (диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам).
Следовательно, проекция отрезка О₁О₂ это отрезок ДМ.
ΔАО₁М - равнобедренный (О₁А=О₁М), значит О₁Д - высота, медиана и биссектриса.
Значит АД=ДМ
По условию АС=2АМ=2*2ДМ=4ДМ, ч.т.д
б) О₁А=5, О₂С=17, АС=16
Значит АД=ДМ=16/4=4, АМ=МС=8
Из прямоугольного ΔАО₁Д:
О₁Д=√(О₁А²-АД²)=√25-16=3
Из прямоугольного ΔАО₂М:
О₂М=√(О₂А²-АМ²)=√289-64=15
Продолжим О₂М до пересечения прямой О₁К, параллельной АС (К-точка пересечения). Полученный четырехугольник О₁ДМК - прямоугольник (О₁Д=МК=3, О₁К=ДМ=4)
О₂К=О₂М+МК=15+3=18
Из прямоугольного ΔО₁О₂К:
О₁О₂=√(О₁К²+О₂К²)=√(16+324)=√340=2√85
и еще вариант:
центр О₁ мог лежать и внутри окружности с центром О₂ (внутри ΔАО₂М)
тогда О₂К=О₂М-МК=15-3=12
Из прямоугольного ΔО₁О₂К:
О₁О₂=√(О₁К²+О₂К²)=√(16+144)=√160=4√10