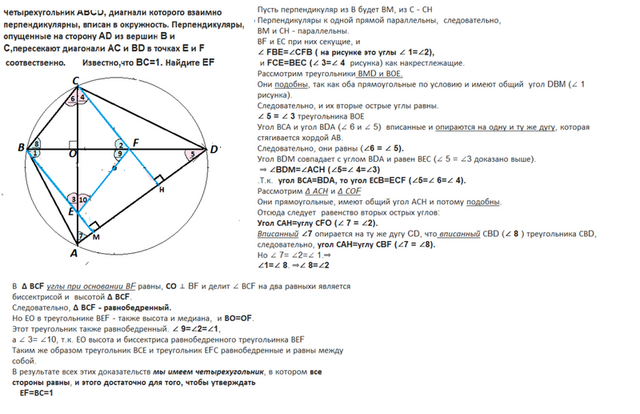
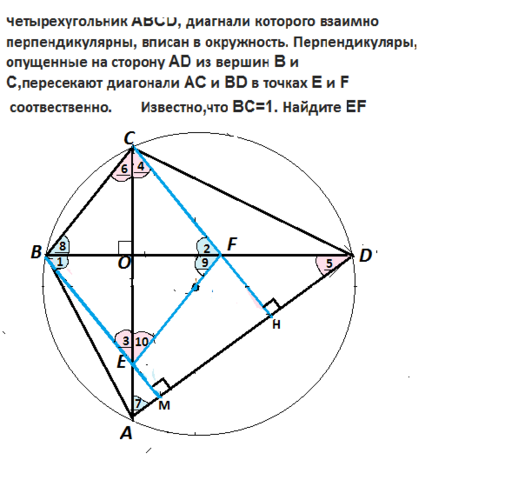
Сделаем рисунок.
Пусть перпендикуляр из В будет ВМ, из С - СН
Перпендикуляры к одной прямой параллельны, следовательно,
ВМ и СН - параллельны.
ВF и ЕС при них секущие, и
∠ FBE=∠CFB ( на рисунке это углы ∠ 1=∠2),
и FCE=BEC (∠ 3=∠ 4 рисунка) как накрестлежащие.
Рассмотрим треугольники ВМD и ВОЕ.
Они подобны, так как оба прямоугольные по условию и имеют общий угол DBM (∠ 1 рисунка).
Следовательно, и их вторые острые углы равны.
∠ 5 = ∠ 3 треугольника ВОЕ
Угол ВСА и угол ВDА (∠ 6 и ∠ 5) вписанные и опираются на одну и ту же дугу, которая стягивается хордой АВ.
Следовательно, они равны (∠6 = ∠ 5).
Угол ВDМ совпадает с углом ВDА и равен ВЕС (∠ 5 = ∠3 доказано выше). ⇒ ∠BDМ=∠ACH (∠5=∠ 4=∠3)
.Т.к. угол ВСА=BDA, то угол ЕСB=ECF (∠5=∠ 6=∠ 4).
Рассмотрим Δ АСН и Δ СОF
Они прямоугольные, имеют общий угол АСН и потому подобны.
Отсюда следует равенство вторых острых углов:
Угол САН=углу СFO (∠ 7 = ∠2).
Вписанный ∠7 опирается на ту же дугу CD, что вписанный СBD (∠ 8 ) треугольника СВD, следовательно, угол СAH=углу СBF (∠7 = ∠8).
Но ∠ 7= ∠2=∠ 1.⇒
∠1=∠ 8. ⇒∠ 8=∠2
В Δ ВСF углы при основании ВF равны, СО ⊥ BF и делит ∠ ВСF на два равныхи является биссектрисой и высотой Δ ВСF.
Следовательно, Δ ВСF - равнобедренный.
Но ЕО в треугольнике ВЕF - также высота и медиана, и ВО=ОF.
Этот треугольник также равнобедренный. ∠ 9=∠2=∠1,
а ∠ 3= ∠10, т.к. ЕО высота и биссектриса равнобедренного треугольинка ВЕF
Таким же образом треугольник ВСЕ и треугольник ЕFС равнобедренные и равны между собой.
В результате всех этих доказательств мы имеем четырехугольник, в котором все стороны равны, и этого достаточно для того, чтобы утверждать равенство ЕF=ВС=1
( Даны 2 рисунка - один с решением, другой - без)
------------
[email protected]