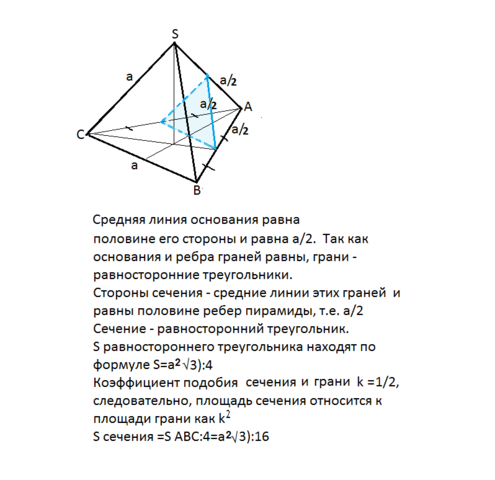
Пирамида называется правильной,
если её основание -правильный n-угольник, а все боковые рёбра равны.
Т.е. боковые грани - равнобедренные треугольники. По условию стороны основания и боковые ребра равны
а, следовательно,
боковые грани - не просто равнобедренные, но и
правильные треугольники.
Средняя линия треугольника равна половине стороны, которой она параллельна.
Сечение - треугольник. Его боковые стороны также средние линии боковых граней. Следовательно, это сечение - равносторонний треугольник Сечение и грани пирамиды - подобные треугольники с коэффициентом подобия 1/2.
Площадь правильного треугольника находят по формуле
S=(а²√3):4.
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Площадь сечения пирамиды относится к площади грани как k²=
(1/2)²=1/4
Sсеч. =S АВС
:4
Sсеч. =(а²√3):16