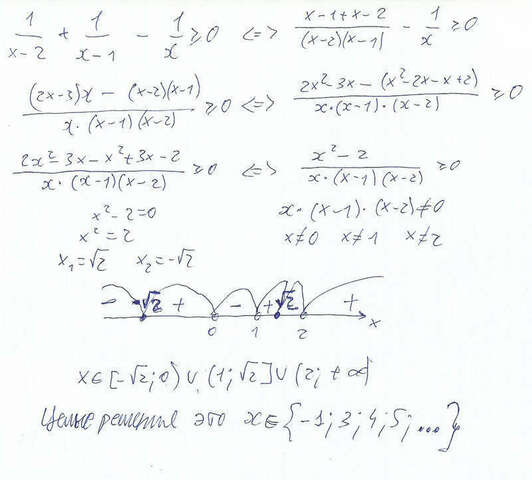\frac{ x^{2} -2x+6-x(x+1)}{x+1} \geq 0 <=> \frac{ -3x+6}{x+1} \geq 0 " alt=" \frac{ x^{2} -2x+6}{x+1} -x \geq 0 <=> \frac{ x^{2} -2x+6-x(x+1)}{x+1} \geq 0 <=> \frac{ -3x+6}{x+1} \geq 0 " align="absmiddle" class="latex-formula"> Получаем, что:
-3x+6=0 <=> x=2,
и x+1≠0 <=> x≠-1
Дробь будет неотрицательной на промежутке x∈(-1;2]
Значит, целыми решениями первого неравенства будут иксы: 0; 1; 2.
Второе неравенство решено в файле