Исследуйте функцию f(х)=х^3-3х^2+4 И Исследуйте функцию f(х)=х^3-3х^2+4 И постройте ее...

$y=f(x)=x^3-3x^2+4, \\ 1) \ D_y=R, \\ 2) \ E_y=R,$
$3) \ f(-x)=(-x)^3-3(-x)^2+4=-x^3-3x^2+4=-(x^3+3x^2-4), \\f(-x)\neq f(x), \\ f(-x)\neq -f(x);$
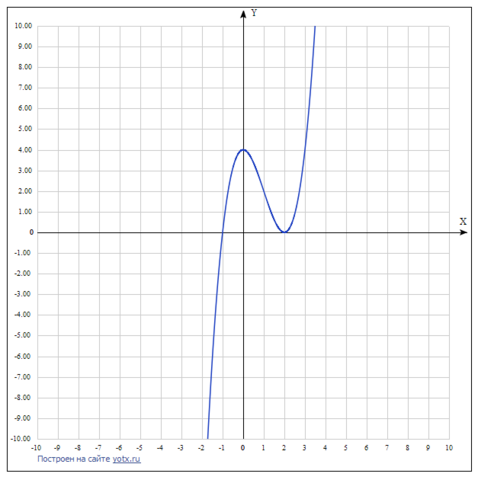
функция общего вида (ни четная ни нечетная);
$4) \ x=0, f(0)=0^3-3\cdot0^2+4=4, \\ y=0, x^3-3x^2+4=0, \\ x^3-2x^2-x^2+2x-2x+4=0, \\ x^2(x-2)-x(x-2)-2(x-2)=0, \\ (x-2)(x^2-x-2)=0, \\ x-2=0, x_1=2, \\ x^2-x-2=0, x_2=-1, x_3=2; \\ (0;4), (-1;0), (2;0);$
нули функции;
$5)\ y=x^3-3x^2+4=(x+1)(x-2)^2, \\ y\gtrless0, (x+1)(x-2)^2\gtrless0, \\ (x-2)^2\geq0 \ x\in R, \\ x+1\gtrless0, \\ x\gtrless-1, \\ x\ \textless \ -1, x\in(-\infty;-1) \ \ y\ \textless \ 0, \\ x \geq -1, x\in[-1;+\infty) \ \ y \geq 0;$
промежутки знакопостоянства функции;
$6) \ f'(x)=(x^3-3x^2+4)'=3x^2-6x, \\ f'(x)=0, 3x^2-6x=0, \\ x(x-2)=0, \\ x_1=0, x_2=2; \\ f(0)=4, f(2)=0; \\ (0;4), (2;0);$
критические точки функции;
$f'(x)\gtrless0, 3x^2-6x\gtrless0, \\ x(x-2)\gtrless0, \\ x\ \textless \ 0, x\in(-\infty;0) \ \ f'(x)\ \textgreater \ 0 \ \ y\nearrow, \\ 0\ \textless \ x\ \textless \ 2, x\in(0;2) \ \ f'(x)\ \textless \ 0 \ \ y\searrow, \\ x\ \textgreater \ 2, x\in(2;+\infty) \ \ f'(x)\ \textgreater \ 0 \ \ y\nearrow,$
промежутки возрастания и убывания функции;
$x_{max}=0, x_{min}=2, \\ (0;4), (2;0);$
точки экстремумов;
$7) \ \ f''(x)=(3x^2-6x)'=6x-6, \\ f''(x)=0, 6x-6=0, \\ x=1, \\ f(1)=1^3-3\cdot1^2+4=2, \\ (1;2)$
точка перегиба функции;
$f''(x)\gtrless0, 6x-6\gtrless0, \\ x\gtrless1, \\ x\ \textless \ 1, x\in(-\infty;1) \ \ f''(x)\ \textless \ 0 \ \ y\frown, \\ x\ \textgreater \ 1, x\in(1;+\infty) \ \ f''(x)\ \textgreater \ 0 \ \ y\smile;$
промежутки выпуклости вогнутости;
$8) \ \lim\limits_{x \to +\infty} f(x) = \lim\limits_{x \to +\infty} f(x) = \lim\limits_{x \to +\infty} x^3-3x^2+4 = +\infty; \\ \lim\limits_{x \to -\infty} f(x) = \lim\limits_{x \to -\infty} f(x) = \lim\limits_{x \to -\infty} x^3-3x^2+4 = -\infty; \\ x \to +\infty \ \ y \to +\infty, \\ x \to -\infty \ \ y \to -\infty.$

x - одно из слагаемых, 12-х - второе слагаемое.
$x \geq 0, 12-x \geq 0, \\ x \leq 12, \\ 0 \leq x \leq 12, x\in[0;12]; \\ p(x)=x^2\cdot2(12-x)=2x^2(12-x), \\ p'(x)=(2x^2(12-x))'=(24x^2-2x^3)'=48x-6x^2, \\ p'(x)=0, 48x-6x^2=0, \\ x(8-x)=0, \\ x_1=0, x_2=8; \\ p(0)=0^2\cdot2(12-0)=0, \\p(8)=8^2\cdot2(12-8)=8^3=512, \\ p(12)=12^2\cdot2(12-12)=0, \\ \max\limits_{x\in[0;12]}2x^2(12-x) = 512, x=8; \\ 12-x=4; \\ 12=8+4.$