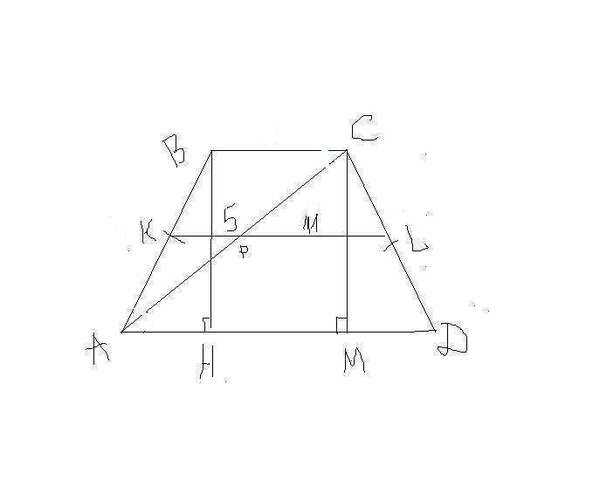
Дано:
ABCD-трапеція
AB=CD=12 см
AC-діагональ
KL-середня лінія
КP=5cm PL=11 cm
Знайти: кути трапеції
Розв`язання
КP-середня лінія ΔABC(паралельна третій стороні). BC=2*KP=2*5=10cm
KL=KP+PL=5+11=16(cm) Оскільки KL-середня лінія трапеції,то вона дорівнює півсумі основ. BC+AD=KL*2=32 AD=32-10=22
Проведемо висоти ВН і СМ. ВНМС-прямокутник(усі кути по 90⁰)
НМ=ВС=10см(як протилежні сторони прямокутника)
ΔBHA і ΔСМD рівні(AB=CD , AH=MD як проекції похилих, кут A=кут D як кути рівнобедренної трапеції)
АН=(AD-HM)/2=(22-10)/2=6(cm)
З ΔBHA(H=90⁰) знайдемо кут А через косинус
cosA=AH/AB=6/12=1/2
Кут А=60⁰
Кут D=60⁰
Кут А+B=180° (ABCD-трапеція)
В=120⁰ і С=120⁰ аналогічно
Відповідь: 120⁰,60⁰,120⁰,60⁰