Площа рівнобедреного трикутника дорівнює 768см, а його основа 48см. Точка в просторі...

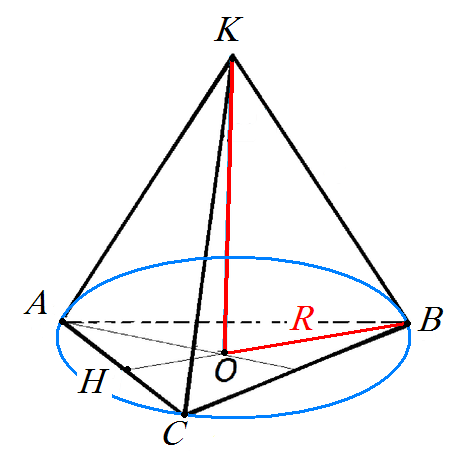
Дано:
S = 768 см²
(AC) = 48 см.
(KO) = 60 см.
(AB) = (BC)
Найти : (KA) = (KB) = (KC)

Решение
Построим высоту к основанию (АС), тогда из свойств равнобедренного треугольника, (BH) - медиана и биссектриса угла АВС и делит (АС) пополам ⇒
⇒ (AH) = (HC) = $\frac{1}{2} (AC) = \frac{48}{2} = 24$ см.
Зная формулу :
$S = \frac{1}{2}ah_{a}$ , находим
$h_{a}$ = (BH) = $\frac{2S}{(AC)}$ = $\frac{2*768}{48} = 32$ см.
Так как ΔAHB - прямоугольный, то по теореме Пифагора можно найти катет (AB), который будет равен другому катету (BC) - по условию
$(AB) = \sqrt{ (BH)^{2} + (AH)^{2} } = \sqrt{ 32^{2}+ 24^{2} } = \sqrt{1024+576} =$ 40 см.
По формуле радиуса описанной окружности:
$R= \frac{abc}{4S}$ , где R = (OB) ; а = (АВ) ; b = (BC) ; с = (АС),
находим (OB) = $\frac{40*40*48}{4*768} = \frac{76800}{3072}= 25$ см.
Так как Δ KOB -прямоугольный, то можно найти (KB) по теореме Пифагора:
$(KB)= \sqrt{ (KO)^{2} + (BO)^{2} } = \sqrt{ 60^{2} + 25^{2} } = \sqrt{3600+625} =65$ см. ⇒
⇒ (KB) = (KA) = (KC) = 65 см.
Ответ: (KB) = (KA) = (KC) = 65 см.