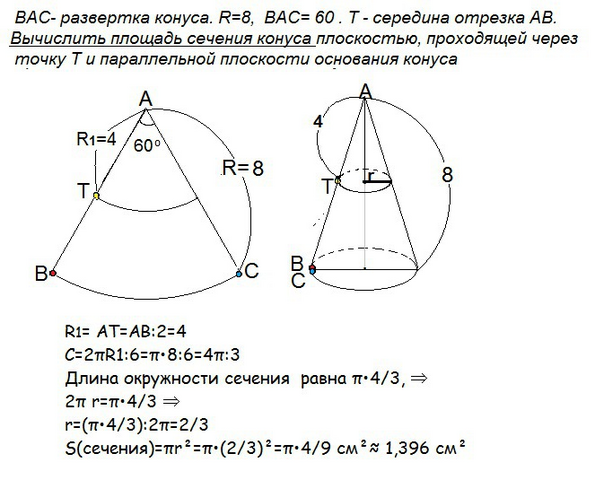
Сектор круга "сворачивается" в прямой конус. Сечение прямого конуса, параллельное основанию - круг.
Площадь круга равна πr².
Так как Т середина АВ, то АТ - радиус меньшего сектора с той же градусной мерой, но другой длиной дуги.
Радиус r сечения найдем из длины дуги меньшего сектора, которая равна 1/6 длины окружности, т.к. длина дуги 60º- шестая часть любой окружности (360º:60º=6).
R1= АТ=АВ:2=4
С=2πR1:6=π•8:6=4π:3
Длина окружности сечения равна π•4/3, ⇒
2π r=π•4/3 ⇒
r=(π•4/3):2π=2/3
S(сеч)=πr²=π•(2/3)²=π•4/9 см²≈ 1,396 см²
---------------
Задачу можно решить, применив отношение площадей подобных фигур. В таком случае узнается радиус основания круга, затем его площадь.
Так как Т - середина образующей конуса, то k=1/2
Отношение площадей подобных фигур равно k², и площадь сечения будет в 4 раза меньше площади основания конуса.