Из постулатов геометрии:
а) Через три точки, не лежащие на одной прямой,
б) через прямую и точку вне ее,
в) через две пересекающиеся прямые,
г) через две параллельные прямые можно провести плоскость и притом только одну.
Если 1 точка не лежит на прямой, а остальные три ( и сколько угодно других) - лежат на прямой. то
можно провести плоскость, и все четыре будут лежать в ней, единственной. Т.е. в этом случае будет соблюдено условие:
через прямую и точку вне ее можно провести плоскость.
В данном случае , поскольку
не все точки лежат в одной плоскости, на прямой не могут лежать три из данных точек. Иначе плоскость можно было бы провести
через точку и прямую, и все 4 точки лежали бы в одной плоскости.
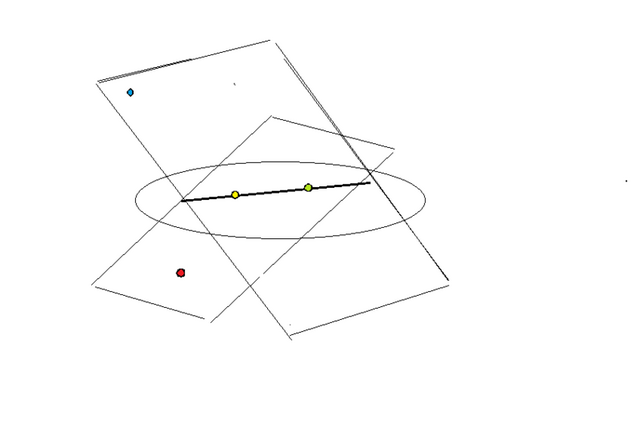
Прямая с двумя точками на ней и две точки вне ее, расположенные в разных плоскостях - таким будет чертеж к этой задаче. .