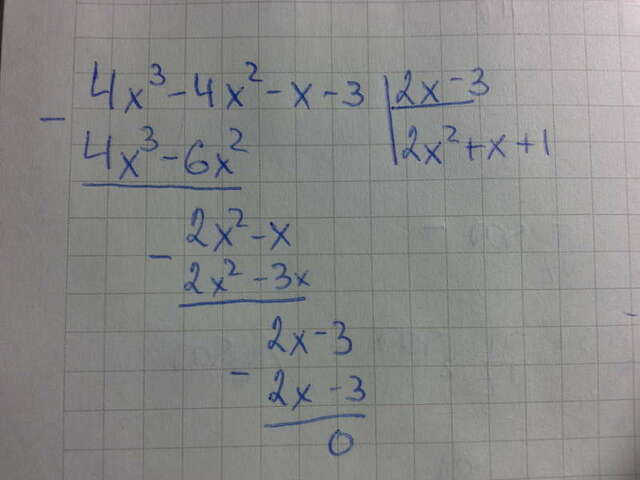4х³-4х²-х-3=0 Помогите, пожалуйста

Question

Дано ответов: 2

аноним · Answer 1 · 2018-04-02T17:21:30+0000

$4x^3-4x^2-x-3=0$

Перед нами уравнение 3-й степени.
Такие уравнение решаются методом деления кубического уравнения на корень этого уравнения(это позволит нам его разложить на множители), либо пытаться что-то вынести за скобку.
Мы будем идти по первому варианту.
Корень уравнения следует искать среди делителей свободного члена, тоесть 3-ки. При этом если у нас перед x^3 стоит какой-то коэффициент(в нашм случае 4-ка), то все делители тройки еще делятся на делители этого коэффициента.
Много слов, ничего не понятно, перейдем к делу.

Делители 3-ки: $б1,б3$
Делители 4-ки: $б1,б2,б4$
И того, корни этого уравнения лежат среди этих чисел: $б1,б\frac{3}2,б\frac{1}2,б\frac{1}4,б\frac{3}4,б3$

Всегда советую в первую очередь подставлять 1 и -1.

$x=1$
$4-4-1-3=0$
$-4 \neq 0$
$x=-1$
$-4-4+1-3=0$
$-10 \neq 0$

Если с 1 и -1 не прокатило, начинается "геморрой". Извиняюсь за свою вольность, но это так.
Придется перебирать дробные корни. Терпение, и у нас все получится.
Пойдем по порядку:

$x=\frac{3}2$
$4*(\frac{3}2)^3-4*(\frac{3}2)^2-\frac{3}2-3=0$
$4*\frac{27}8-4*\frac{9}4-\frac{3}2-\frac{6}2=0$
$\frac{27}2-\frac{18}2-\frac{3}2-\frac{6}2=0$
$\frac{27-18-3-6}2=0$
$\frac{0}2=0$
$0=0$

Ура. Мы нашли 1-ый корень. Но не забываем, что у кубического уравнения, возможно, есть еще 2 корня. :)
Делим весь наше уравнение на этот корень(см. вложение)

В итоге, вот что у нас вышло: $(2x-3)(2x^2+x+1)=0$
$2x^2+x+1=0$
$D=1-2*4\ \textless \ 0$

Корней у квадратного трехчлена нет. Поэтому ответ всего один.

Ответ: $\frac{3}2$

P.s Обычно кубические уравнения сделаны проще, и корень сразу находится среди 1(-цы) и -1(-цы).