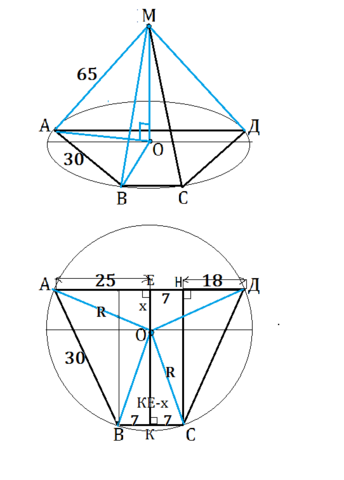
Основания равнобедренной трапеции равны 14 и 50 см, боковая сторона - 30 см. Вычислите расстояние от площади трапеции до точки, равноудаленной от каждой из вершин на 65 см.
Обозначим равноудаленную от каждой из вершин точку буквой М.
Отрезки, соединяющие точку М с вершинами трапеции - равные наклонные, следовательно, их проекции тоже равны и совпадут с центром описанной вокруг данной трапеции окружности с радиусом, равным проекциям этих наклонных.
Сделав рисунок и соединив точку М с вершинами трапеции, получим пирамиду с высотой МО, длина которой и есть искомое расстояние ( расстояние от точки до плоскости - перпендикуляр), и основанием пирамиды - данной трапецией.
Нарисуем основание с трапецией отдельно и соединим центр окружности О с вершинами трапеции.
Получим равнобедренные треугольники АОД и ВОС.
Расстояние между основаниями трапеции АД и ВС равно высоте НС трапеции. Найдем длину НС из прямоугольного треугольника СНД.
СН=√(CД²-НД²)
(ДН=АД-ВС):2=18 см
СН=√(900-324)=24 см
Проведем еще одну высоту ЕК через центр окружности.
ЕК=НС=24 см
Пусть расстояние ЕО от центра АД до центра окружности будет х.
Тогда ОК=24-х
Выразим квадрат радиуса описанной окружности из треугольника АОЕ:
R²=25²+х²
Выразим квадрат радиуса описанной окружности из треугольника ВОК:
R²=(24-х)+7² и приравняем эти выражения:
25²+х²=(24-х)+7²
625+х²=576-48х+х²+49
получим
48х=0, ⇒
х=0, из чего следует, что
центр описанной окружности лежит на основании трапеции АД.
Тогда
R=АД
:2=
25 см
Вернёмся к первому рисунку.
Треугольник АОМ - прямоугольный с катетами, равными АО и МО.
АМ²=МО²+АО²
4225=МО²+625
МО=√3600=
60 cм
--------
[email protected]