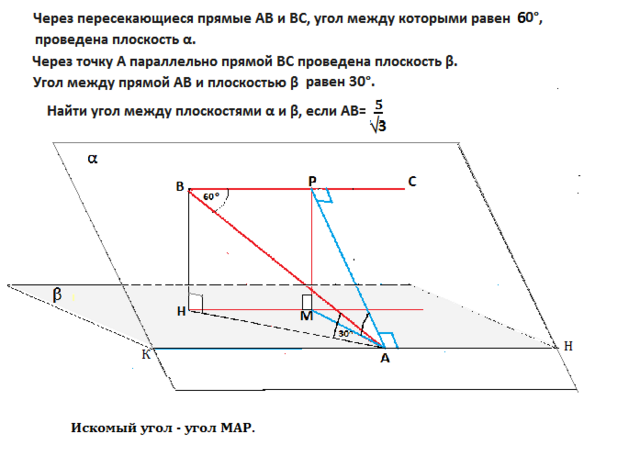
Вопрос задачи - найти величину двугранного угла.
Двугранный угол измеряется величиной его линейного угла.
На рисунке это угол между перпендикулярами АР и АМ, возведенными из точки А к линии пересечения плоскостей, т.е. к ребру КН этого угла.
Угол между прямой АВ и плоскостью β - это угол ВАН, т.е. угол между ВА и ее проекцией АН на плоскость β.
ВН ⊥ плоскости β, следовательно, ⊥ и прямой НМ, проведенной параллельно КН.
Треугольник АВН - прямоугольный, угол НВА= 90º-30º=60º.
ВН=АВ*sin 30º=(5:√3)*1/2=(5:√3)/2
Если плоскость α проходит через прямую a, параллельную плоскости β, и пересекает эту плоскость по прямой b, то b || a.
ВС параллельна плоскости β, которая пересекает плоскость α по прямой КН ⇒
ВС и КН - параллельны.
АР - общий перпендикуляр к ВС и КН, ⇒ треугольник АРВ - прямоугольный. АР=АВ*sin 60º=(5:√3)*√3):2=5/2
Из Р опустим перпендикуляр РМ на плоскость β
РМ || ВН ⇒ РМ=ВН =(5:√3)/2
Треугольник РАМ - прямоугольный.
АМ - проекция АР на плоскость β , АР⊥КН.
По т. о трех перпендикулярах АМ ⊥ КН, ⇒
∠ РАМ - линейный угол двугранного угла между плоскостями α и β.
sin ∠РАМ = РМ:АР={(5:√3)/2 }:5/2=1/√3 =0,57735 ≈ 0,5774
По таблицам Брадиса это синус угла 35º16'