Много много баллов)) Остальные задачи у меня в профиле)) Основание и боковая сторона...

Question

Много много баллов)) Остальные задачи у меня в профиле))
Основание и боковая сторона равнобедренного треугольника равны 26 и 38 соответственно.
а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.
б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.

Answer 1

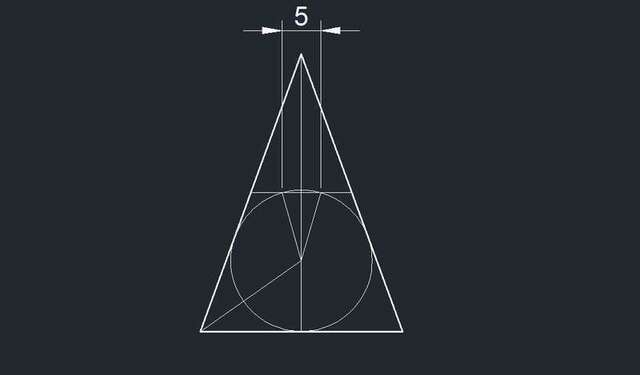
А) Высота на основание равна H =√(38²-(26/2)²) = √(1444-169) = √1275 =  35.70714. Разделив на 2, получим половину высоты h = 17,85357. Средняя линия пересекает высоту именно в этом месте.
Теперь найдём радиус вписанной окружности:
r = √((p-a)(p-b)(p-c)/p) = √(( 51-38)( 51-26)( 51-38)/ 51) = 9,10182055.
2 радиуса (диаметр) равны 2r = 2* 9,10182055 = 18,2036411.
Это доказывает, что средняя линия пересекает вписанную окружность.

б) Величина стрелки (это высота сегмента) равна Δ = 2r - h = 18,2036411 - 17,85357 =  0.35007002.
Длина отрезка  средней линии, заключённого внутри окружности, равна L = 2√(r²-(r-Δ)²) = √(9,10182055²-(9,10182055-  0.35007002)²) =2√6.25 = 2*2.5 = 5.

---