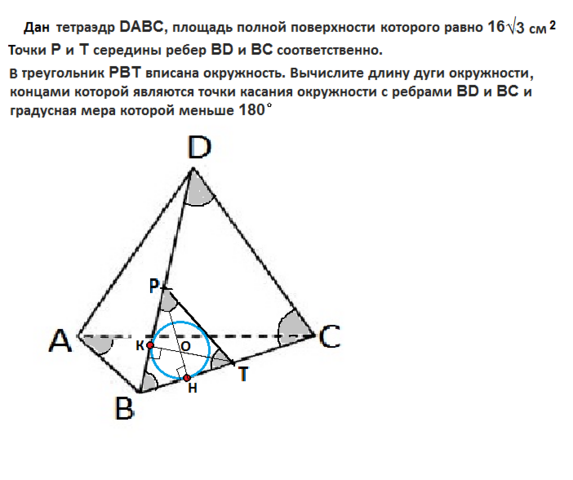
Поскольку других размеров не дано, надо думать, данный тетраэдр - правильный.
Следовательно, все его 4 грани - правильные треугольники, а
площадь одной грани равна 16√3:4=4√3
Площадь правильного треугольника находят по формуле
S=(а²√3):4
4√3=(а²√3):4, откуда
а=4. т.е. ребро данной пирамиды равно 4.
Тогда треугольник ВРТ тоже правильный, т.к. Р и Т - середины ребер, и стороны треугольника ВРТ равны2.
Пусть точки касания вписанной в него окружности будут
на ребре BD -К, на ребре ВС -Н
В четырехугольнике КВНО углы при К и Н - прямые, угол В=60°.
Т.к. сумма углов четырехугольника равна 360°, а
сумма углов К и Н=90°*2=180°, то
угол КОН равен 180°- 60°=120°.
Т.е. дуга КН=120°, и ее длина равна 360°:120°=одной трети длины вписанной в треугольник ВРТ окружности.
Радиус вписанной в правильный треугольник окружности а:2√3
Радиус данной вписанной окружности 2:2√3=1/√3 см
Длина этой окружности L=2πr=2π:√3 см
Длина дуги градусной мерой 120° равна одной трети длины всей окружности.
Следовательно, длина дуги
КН=(2π:√3):3 или (2π√3):9 см