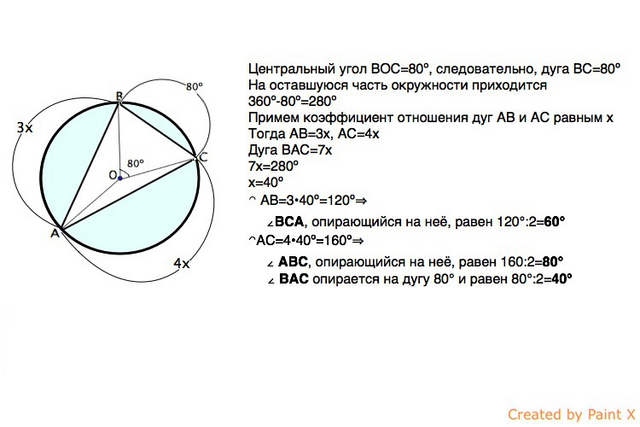
Центральный угол ВОС=80º, следовательно, дуга ВС=80º
На оставшуюся часть окружности приходится
360º-80º=280º
Примем коэффициент отношения дуг АВ и АС равным х
Тогда АВ=3х, АС=4х
Дуга ВАС=7х
7х=280º
х=40º
◠ АВ=3•40º=120º⇒
вписанный ∠ВСА, опирающийся на неё, равен 120°:2=60°
◠AC=4•40º=160º⇒
вписанный ∠ АВС, опирающийся на неё, равен 160:2=80°
Вписанный ∠ ВАС опирается на дугу 80° и равен 80°:2=40°
∠ВАС+ ∠ВСА+ ∠ АВС=40°+60°+80°=180° - решение верно.