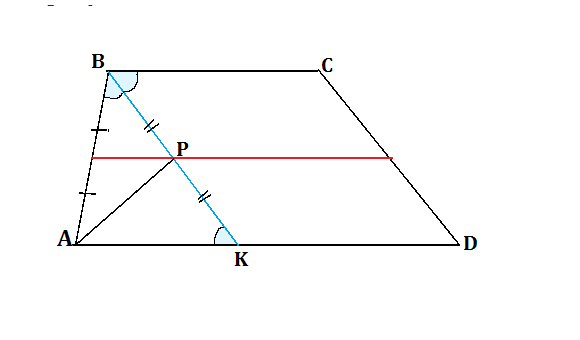
В трапеции ABCD (AD II BC) биссектриса угла ABC пересекает среднюю линию в точке P. Докажите, что угол APB = 90 градусов.
--
Биссектриса делит угол АВС пополам.
Пусть она пересекает АД в точке К.
Угол СВК равен углу ВКА как накрестлежащий. Но СВК=АВК по условию ⇒ углы пи ВК равны, и треугольник ВАК - равнобедренный.
Средняя линия трапеции является и средней линией треугольника АВК и делит стороны пополам.
ВР=РК.⇒ АР - медиана треугольника ВАК.
Так как в равнобедренном треугольнике медиана является и биссектрисой, и высотой, АР - выстоа, перпендикулярна ВК и угол АРВ=90º