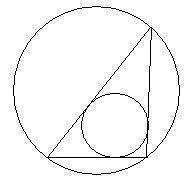
Пожалуйста помогите с задачой ? Зная координаты вершин треугольника в пространстве,...

Question

Пожалуйста помогите с задачой ?

Зная координаты вершин треугольника в пространстве, определите отношение площади вписанной в него окружности к площади описанной окружности вокруг этого же треугольника.
нам известны x1 , y1 , z1 , x2 , y2 , z2 , x3 , y3 , z3
пример 0 0 0 0 0 1 0 1 0 ответ 0.172
формулу или решение покажите ?

---

Answer 1

Стороны треугольника находим по формуле:
  d =√((х2 - х1 )² + (у2 - у1 )² + (z2 – z1 )²).
Получаем длины: 1, √2 и 1.
Зная стороны, находим радиусы:
- вписанной окружности r = √((p-a)(p-b)(p-c)/p).
a              b            c                   p                            2p
1     1.4142136    1          1.7071068           3.414213562
r = 0.2928932 Sr =  0.269506.
- описанной окружности R = abc / (4√(p(p-a)(p-b)(p-c)).
a             b          c              p                     2p                                
1    1.4142136  1     1.7071068    3.414213562 
R = 0.707106781       S = 1.570796
Sr /S = 0.171573
Можно добавить, что треугольник прямоугольный с острыми углами по 45 градусов.