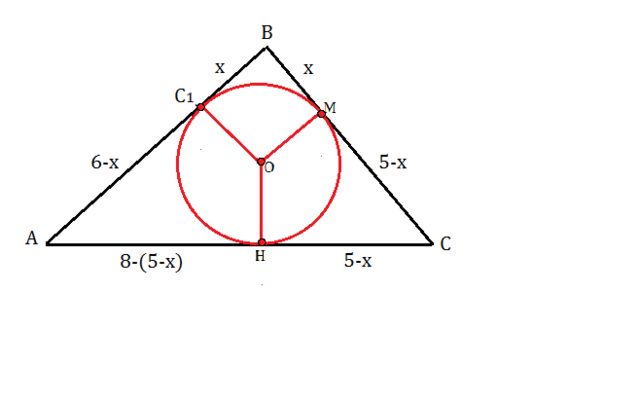
В треугольнике АВС вписанная окружность касается его сторон в точках С1, М, Н.
О - центр окружности.
По свойству равенства отрезков касательных из одной точки к окружости АС₁=АН,
ВС₁=ВМ,
СМ=СН.
Пусть отрезок ВС₁ и КМ=х.
Тогда АС₁=6-х, СМ=5-х, АН=8-(5-х)
Так как АС₁=АН, составим уравнение:
6-х=8-5+х
3=2х
х=1,5
АС₁=6-1,5=4,5