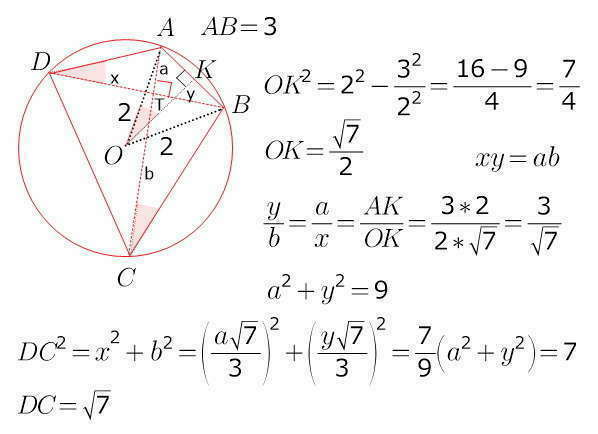
Известна одна только сторона...
она связана с радиусами описанной окружности в равнобедренный треугольник, если в этом треугольнике провести высоту к основанию, то
мы получим угол (половину центрального угла), равный двум вписанным углам: АОК = АСВ = ADB
эти вписанные углы --острые углы прямоугольных треугольников
СТВ и DTA ((T ---точка пересечения диагоналей 4-угольника)))
диагонали ---хорды окружности, пересекающиеся хорды
произведения отрезков пересекающихся хорд равны)))
на рис. эти отрезки для краткости обозначены маленькими буквами...
отношение этих отрезков можно вычислить (это будет тангенс уже описанных равных углов tg(АОК) = tg(ACB) = tg(ADB)
остальное по т.Пифагора из прямоугольных треугольников)))