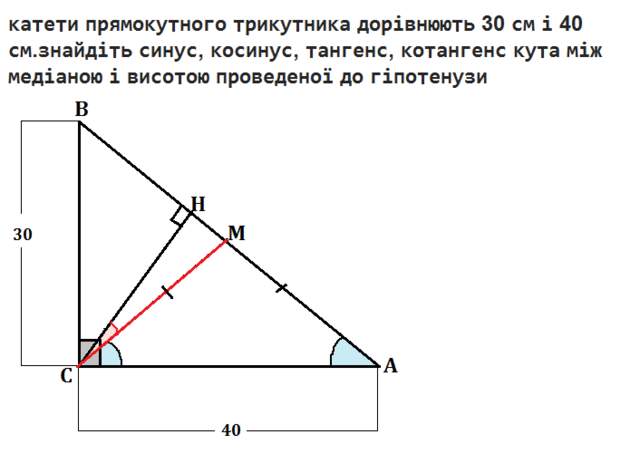
Катеты прямоугольного треугольника равны 30 см и 40 см. Найдите синус, косинус, тангенс, котангенс угла между медианой и высотой, проведенных к гипотенузе.
---------
Пусть дан треугольник АВС.
ВС=30 см,
АС=40 см. Из отношения катетов 3:4 следует, что этот треугольник - египетский, и АМ=50 см ( по т. Пифагора, естественно, также АВ=50 см)
Длина медианы прямоугольного треугольника из прямого угла к гипотенузе равна ее половине. ⇒
СМ=ВМ=АМ=
25 см
∆ АМС - равнобедренный.
Высота прямоугольного треугольника делит его на подобные треугольники.
∆ ВНС~∆ ВСН, коэффициент подобия
k= ВС
:АВ=
0,6 ⇒
ВН=СН*0,6=
18 см
СН=АС*0,6=
24 см
МН=ВМ-ВН=25-18=
7 см
sin ∠HCM=MH:CM=
7/25
cos ∠HCM=CH:CM=
24/25
tg ∠HCM=HM:HC=
7/24
ctg ∠HCM=HC:HM=
24/7