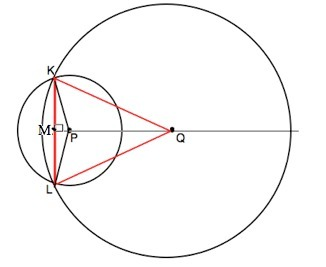
Проведем QP до пересечения с КL в точке М.
∆ КQL равнобедренный ( две стороны - радиусы. )
∆ КРL - равнобедренный ( две стороны - радиусы.),
В треугольниках KРQ и LPQ стороны KP=LP, KQ=LQ. сторона PQ -общая.
∆KO=∆LPQ по третьему признаку равенства треугольников. ⇒
∠КQP=∠LQP, и QM - биссектриса равнобедренного треугольника KQL.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является еще медианой и высотой.⇒
PQ ⊥ KL, что и требовалось доказать.