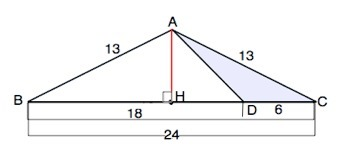
Дан равнобедренный треугольник АВС с боковыми сторонами, равными 13, и основанием ВС.
Точка D делит ВС на отрезки BD=18 и CD=6
ВС=18+6=24.
АН - высота равнобедренного треугольника, значит, и медиана. ВН=СН=24:2=12.
В ∆ АВН отношение катет: гипотенуза=12:13. Это отношение треугольника из Пифагоровых троек, где катеты и гипотенуза – целые числа. Второй катет АН=5. ( Проверьте по т.Пифагора).
АН - общая высота для ∆ АВС и АСD, проведенная из А к основанию.
S=a•h:2
S=6•5:2=15 см²