Средняя линия трапеции, равная 10 см, делит площадь трапеции в отношении 3:5. Найдите длины оснований этой трапеции.
-------
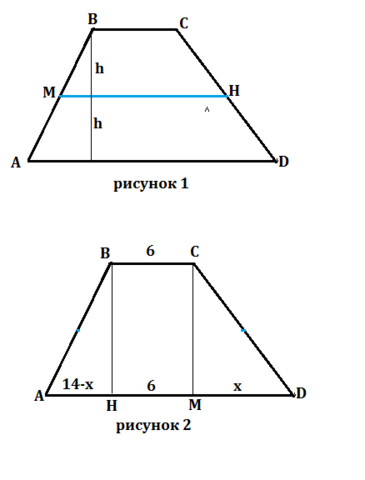
См. рисунок 1 приложения.
В трапеции АВСD средняя линия МН делит её высоту пополам.
Пусть ВС=а, АD=b
Тогда
S MBCH= h*(a+10):2
S AMHD=h*(b+10):2
S MBCH : S AMHD=3:5
[(a+10):2]:[(b+10):2]=3:5
3b+30=5a+50
3b=5a+20
средняя линия трапеции равна полусумме оснований.
(a+b):2=10
а+b=20
b=20-a
3b=60-3a
приравняем значения
3b:5a+20=60-3a
8a=40
a=5
b=20-5=15
BC=5 cм AD=15 см
________________________________________________________________________________
В трапеции длины оснований равны 6 см и 20 см, а длины боковых сторон равны 13 см и 15 см. Найдите площадь трапеции.
-----
См. рисунок 2 приложения.
Опустим из В и С перпендикуляры ( высоты) ВН и СМ на АD.
Тогда НМ=6 см
АН+МD=20-6=14
МD=x, АН=14-x
Из прямоугольного треугольника АВН
ВН²=13²-(14-х)²
Из прямоугольного треугольника СМD
СМ²=15²-х²
ВН=СМ ⇒
13²-(14-х)² = 15²-х²
откуда после вычислений получим
28х=252
х=9
СМ²=15²-9²
СМ=√(225-81)=12
S ABCD=(6+20)*12:2=156 cм²
--------
В треугольнике АВС внешний угол при вершине А равен 125º, а внешний угол при вершине В равен 59º. Найдите угол С. Ответ дайте в градусах.
Внешний и внутренний углы при одной вершине треугольника являются смежными.
Сумма смежных углов равна 180º ⇒
Угол А=180º-125º=55º
Внешний угол при В равен сумме углов А и С.
Угол С=59º-55º=4º