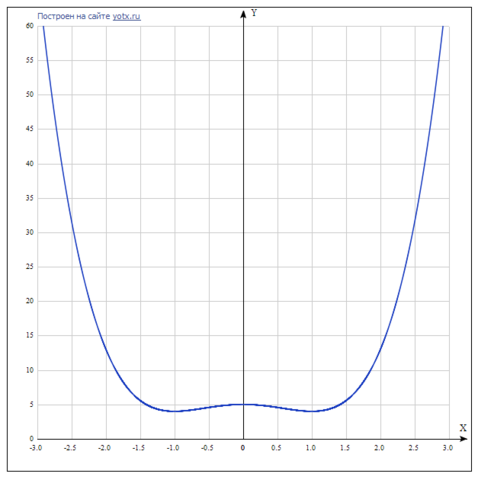
Так как в заданной функции присутствует дробь, то из ОДЗ надо исключить недопустимое значение х = -1.
Теперь можно преобразовать дробь:
х^4-2х^2-(5(х^2-1)/(х+1))+5х == х^4-2х^2-(5(х+1)(х-1)/(х+1))+5х После сокращения на х+1 получаем:х^4-2х^2-5(х-1)+5х =х^4-2х^2-5х+5+5х =х^4-2х^2+5.Находим производную:
f' =4x ³-4x и приравниваем её 0:
4x ³-4x = 0
4х(х²-1) = 0.
Решая это уравнение, находим критические точки:
4х = 0 х₁ = 0
х² - 1 = 0 х² = 1 х = √1 х₂ = 1 х₃ = -1 этот корень отбрасываем.
Теперь определяем, где минимум, а где максимум.
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:Минимумы функции в точках:x2 = 1 Максимумы функции в точках:x2 = 0 Убывает на промежутках (-oo, 0] U [1, oo) Возрастает на промежутках [0, 1]