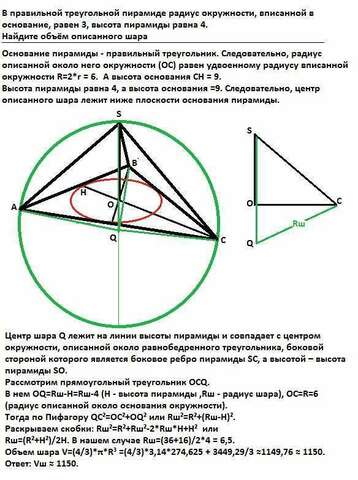
Основание пирамиды - правильный треугольник. Следовательно, радиус описанной около него окружности (ОС) равен удвоенному радиусу вписанной окружности
R=2*r = 6. А высота основания СН = 9.
Высота пирамиды равна 4, а высота основания =9. Следовательно, центр описанного шара лежит ниже плоскости основания пирамиды.
Центр шара Q лежит на линии высоты пирамиды и совпадает с центром окружности, описанной около равнобедренного треугольника, боковой стороной которого является боковое ребро пирамиды SC, а высотой – высота пирамиды SO.
Рассмотрим прямоугольный треугольник ОCQ.
В нем ОQ=Rш-H=Rш-4 (Н - высота пирамиды ,Rш - радиус шара), ОС=R=6 (радиус описанной около основания окружности).
Тогда по Пифагору QC²=ОС²+OQ² или Rш²=R²+(Rш-H)².
Раскрываем скобки: Rш²=R²+Rш²-2*Rш*Н+H² или
Rш=(R²+H²)/2Н. В нашем случае Rш=(36+16)/2*4 = 6,5.
Объем шара V=(4/3)*π*R³ =(4/3)*3,14*274,625 + 3449,29/3 ≈1149,76 ≈ 1150.
Ответ: Vш ≈ 1150.