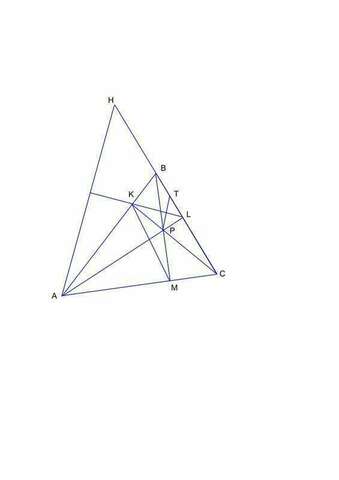
Треугольник BKL имет стороны BL = AB*cos(B) и BK = BC*cos(B) и угол B, общий с треугольником ABC. Поэтому этот треугольник подобен треугольнику ABC с коэффициентом подобия cos(B);
отсюда следует, что KL = AC*cos(B); и ∠KLB = ∠BAC
Точно также доказывается подобие треугольников ABC и AKM (BM - третья высота треугольника ABC) и равенство KM = BC*cos(A).
Поскольку ∠KLB = ∠BAC, то ∠AHL = 90° - ∠KLB = 90° - ∠BAC;
поэтому ∠HAL = ∠TPL = ∠BAC (или просто угол A треугольника ABC);
Легко видеть что HT = HL - TL = AL*tg(A) - PL*tg(A) = AP*tg(A);
HT = AP*sin(A)/cos(A);
Окружность, построенная на AP, как на диаметре, пройдет через точки K и M, то есть будет описанной для треугольника AKM; то есть
AP*sin(A) = KM; (это теорема синусов :)), а (как показано в начале) KM = BC*cos(A);
откуда HT = BC = 6;