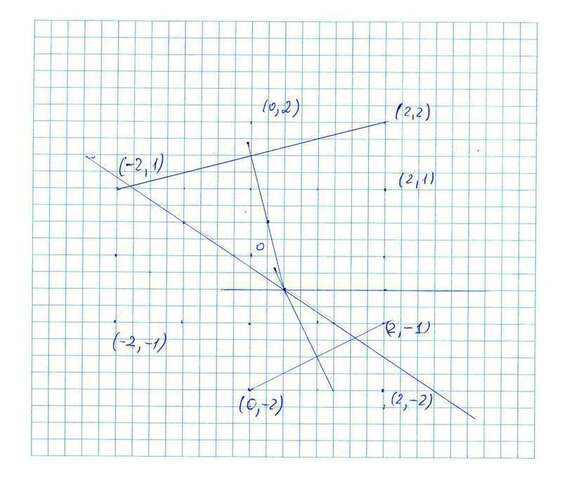
Я помещу начало координат в центр прямоугольника в его первоначальном положении. Кроме того, я буду считать, что прямоугольник не 1х1/2, а 4х2 - для удобства.
Тогда A(-2,-1); B(-2,-1); C(2,1); D(2, -1);
A1 (0,2); B1 (2, 2) C1(2, -2) D1(0, -2);
Точка поворота - это ЦЕНТР ЧЕТЫРЕХ концентрических окружностей, на каждой из которых лежат ОДНОИМЕННЫЕ точки (то есть пары A и A1, B и B1 и так далее); проще всего - с точками C и C1, геометрическое место точек, равноудаленных, от этих двух, лежит на прямой y = -1/2;
кроме того, MC перпендикулярно MC1,
откуда очевидно x = 1/2; (CMC1 - равнобедренный прямоугольный
треугольник, высота = медиане = половине гипотенузы)
Можно, конечно, и взять любую другую пару, и проведя срединный перпендикуляр, легко получить точку M (1/2, -1/2).
Если переместить начало координат в точку M, то координаты углов будут такие
A(-5/2, -1/2); A1(-1/2, 5/2)
B(-5/2, 3/2); B1(3/2, 5/2)
C(3/2, 3/2); C1(3/2, -3/2)
D(3/2, -1/2); D1(-1/2,-3/2)
легко видеть, что в новой системе координат все углы попарно равноудалены от начала координат.
На самом деле, эти точки еще и удовлетворяют условию y' = - x; x' = y; что соответствует повороту ФИГУРЫ на 90°; (или, то же самое, осей на -90°) это означает, что МАЛО ТОГО, что они равноудалены от НОВОГО центра M - группа ABCD целиком переходит в A1B1C1D1 при повороте на 90°. То есть точка M удовлетворяет условию задачи.
В исходных размерах это (1/8, - 1/8); от центра первоначального прямоугольника (это координаты радиус-вектора центра вращения в осях вдоль сторон)
Методологически правильно было бы решать именно так.
Пусть координаты нового начала координат M(a, b); тогда
A(-2 - a, -1 - b); A1(-a, 2 - b);
B(-2 - a, 1 - b); B1(2 - a, 2- b);
C(2 - a, 1 - b); C1(2 - a, -2 - b);
D(2 - a, -1 - b); D1(-a, -2 - b);
Применяя условие, что ABCD переходит в A1B1C1D1 при y1 = -x; x1 = y;
можно получить сразу из пары A и A1
2 - b = - (-2 - a); => b = -a;
-a = -1 - b; => -a = -1 + a; => a = 1/2; b = -1/2;
и надо проверить, что остальные пары точек дают тот же результат.
Хотя, если разобраться, делать этого - не надо :) а почему? :)))
Пусть есть точка A(x, y) и A1(x1,y1), и есть
M(m,n); так что -(x - m) = y1 - n; y - n = x1 - m; найти m и n через x,
y, x1,y1; очень просто. Если теперь взять пару точек B(x + a; y + b) и
B1 (x1 + b; y1 - a); то условие поворота осей на 90° y' = -x; x' = y;
даст те же уравнения, что и для A и A1 - числа a и b сокращаются