1)Для начала рассмотрим ключевой случай - a = 2. Тогда, очевидно, данное неравенство превращается в линейное. И тогда
-x + 1 > 0
-x > -1
x < 1
Замечаем, что все решения неравенства меньше 2(так что хотя бы при одном x < 2 неравенство выполняется). Значит, a = 2 нам подходит.
2)Пусть a отлично от 2. Тогда левая часть неравенства является квадратным трёхчленом, графиком которой, как мы помним, является парабола. А куда направлены её ветви? Это вопрос: это зависит от значения а. Поэтому очевидно, что нам надо сейчас рассмотреть оба этих случая. Это необходимо сделать и потому, что решения неравенства при ветвях параболы, направленных вниз или вверх, решение неравенства принципиально отличается. Итак, нам представляется два случая.
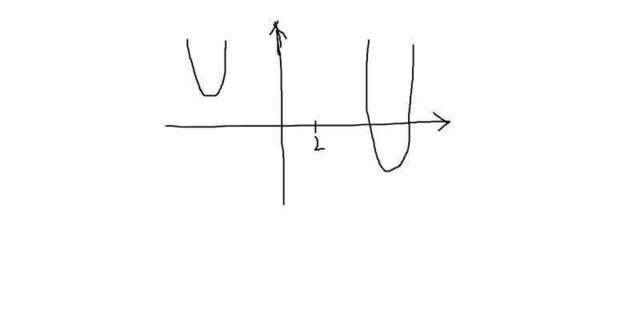
1) Пусть a - 2 > 0, то есть a > 2. Тогда ветви нашей параболы направлены вверх.
Замечаем, что при всех a > 2 условие задачи выполняется. Иллюстрирую рисунком.
Нарисовано несколько парабол различного вида(пересекающих ось OX, не пересекающих её). У всех парабол ветви направлены вверх. При такой ситуации хотя бы для одного x < 2 выполняется положительность квадратного трёхчлена(действительно, на этом интервале хотя бы в одной точке x < 2 f(x) > 0)
2)Пусть теперь a - 2 < 0, то есть, a < 2.
Тогда ветви параболы направлены вниз. Тут уже надо рассматривать несколько случаев.
а)Пусть D < 0. Здесь D - дискриминант квадратного трёхчлена. Тогда парабола находится целиком под осью OX, и неравенство, очевидно, не имеет решений(нет ни одной точки параболы выше оси OX)
б)Пусть D = 0. Ситуация полностью аналогична предыдущей(есть только точка касания с осью OX, но ни одной точки параболы выше неё). Следовательно, этот случай также невозможен.
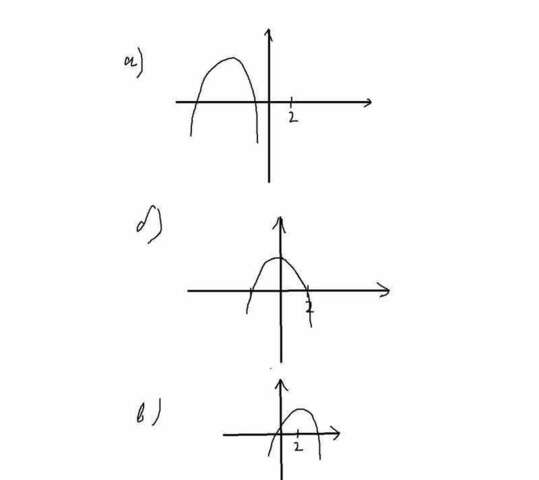
в)Пусть D > 0. Интуиция подсказывает нам, что этот случай возможен. Это произойдёт в следующих ситуациях. Выложил три возможных случая.
1)Пусть сначала первый случай. Оба корня квадратного трёхчлена меньше 2. Это будет, если
D > 0
x0 < 2
f(2) < 0
x0 - абсцисса вершины параболы, f(2) - значение параболы в точке 2.
2)Второй случай выполняется, если f(2) = 0.
3)Здесь f(2) > 0
Осталось найти дискриминант трёхчлена, значение его в точке 2, абсциссу вершины парабол. Подставить в систему их. Решив системы, мы получим искомые значения параметра.