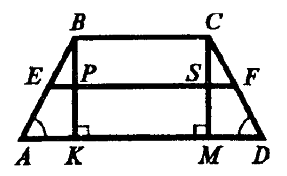
С вершин трапеции опускаем перпендикуляры, получается, что BC=KM=6. => можно найти AK и MD, они равны, т.к трапеция равнобедренная. Будем рассматривать треугольник ABK, найдем AK. AK=(14-6)/2=4. По теореме Пифагора найдем высоту трапеции BK.
BK^2=AB^2-AK^2, подставляем и считаем: 
Теперь найдем площадь трапеции: S=((BC+AD)/2)*BK=((6+14)/2)*3=10*3=30
Ответ: 30