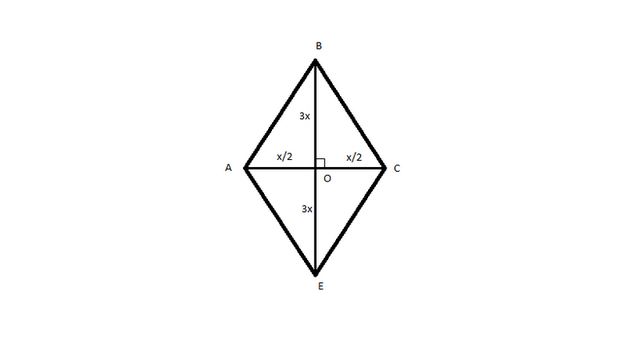
Площадь ромба равна половине произведения его диагоналей. Найдем длину сторон ромба, т к они равны то длину найдем поделив периметр на 4 (12√37 дм/4=3√37 дм).
Диагонали ромба взаимноперпендикулярны и точкой пересечения делятся пополам. Тогда пусть большая диагональ равна 6х, меньшая х. Рассмотрим один из образовавшихся прямоугольных треугольников и по теореме Пифагора найдем половины длинн диагоналей т е ВО=ОС=х/2 (т к АС=х), а ВО=ОЕ=3х (т к ВЕ=6х). По теореме Пифагора:
9х^2+х^2/4=333; домножим на 4 и получим:
36х^2+x^2=1332;
37x^2=1332;
x^2=36
x=6дм, тогда ВЕ=6х=36дм=360см, а АС=х=6дм=60см
Площади ромба=1/2*ВЕ*АС=1/2*360*60=10800см^2=108дм^2
ОТВЕТ:3)108 дм в кв