Расстояние от точки до прямой измеряется перпендикуляром.
Расстояния от М до сторон треугольника - равные по длине наклонные. Следовательно, их проекции на плоскость треугольника также равны, и равны они радиусу вписанной в этот треугольник окружности..
Пусть данный треугольник будет АВС с прямым углом С.
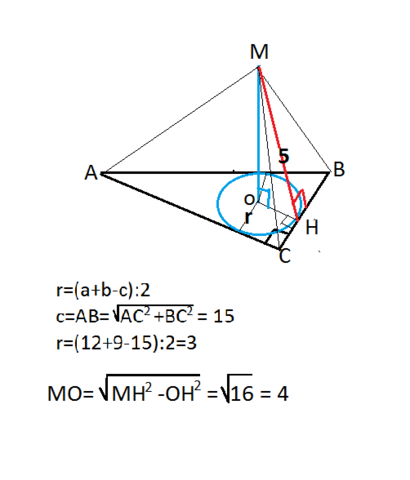
Тогда все отрезки из М, перпендикулярные его сторонам, равны МН=5 см, а основание перпендикуляра МО из М к плоскости треугольника - центр вписанной окружности.
Радиус вписанной окружности найдем по формуле:
r=(a+b-c):2,
где а и b- катеты, с - гипотенуза.
Гипотенузу АВ найдем по т.Пифагора, и равна она 15 см (вычислить сможет каждый, хотя можно устно найти, т.к. треугольник АВС имеет отношение катетов 3:4, и он - египетский)
r=(12+9-15)^2=3 cм
Треугольник МОН - египетский, и
МО=4 см
( можно проверить по т.Пифагора)