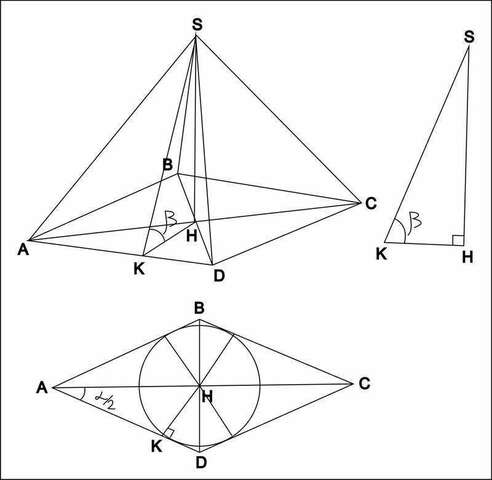
А)если высота пирамиды H, то КН=Н/tgбетта
это действенно для каждой боковой грани пирамиды, высота везде одинаковая и двугранный угол тоже
то есть точка Н равноудалена от сторон основания
то есть точка Н является центром вписанной в ромб окружности
центр вписанной в ромб окружности лежит на биссетрисах углов, то есть на пересечении диагоналей ромба
б)величины получаются с помощью тригонометрических функций прямоугольного треугольника
sin(альфа/2)=КН/АН
КН=Н/tgбетта
АН=Н/(tgбетта*sin(альфа/2))
tg(альфа/2)=HD/AH
HD=H/(tgбетта*cos(альфа/2))
S(основания)=2*(Н/(tgбетта*sin(альфа/2)))*(H/(tgбетта*cos(альфа/2)))=(4H^2)/(tg^2(бетта)sinальфа)
AD=H/(tgбетта*sin(альфа/2)*cos(альфа/2))=2Н/(tgбетта*sinальфа)
Площадь каждой боковой грани равна
S (боковой поверхности)=4*(1/2)*(Н/sinбетта)*(2Н/(tgбетта*sinальфа))=(4Н^2)/(tgбетта*sinальфа*sinбетта)
S(общая)=(4Н^2(sinбетта+tgбетта))/(tg^2(бетта)*sinальфа*sinбетта)