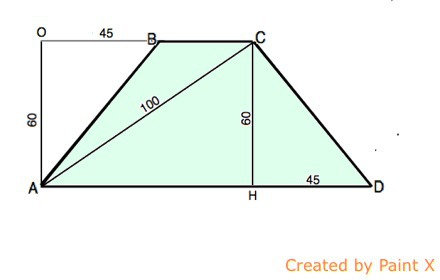
Пусть в данной трапеции основания ВС и АD.
Определение: Высота трапеции — расстояние между прямыми, на которых лежат основания трапеции, т.е. любой общий перпендикуляр этих прямых.
Тогда высота СН, опущенная из С на AD, равна АО=60 мм.
Высота равнобедренной трапеции, опущенная из тупого угла, делит основание на отрезки, больший из которых равен длине средней линии трапеции.
АН=средней линии трапеции.
Т.к. ∆ АСН прямоугольный и отношение катета к гипотенузе равно 3:5, этот треугольник из троек Пифагора ( египетский), АН=80 мм ( и по т.Пифагора получим тот же результат)
Тогда АН равна длине средней линии.
Площадь трапеции равна произведению высоты на среднюю линию, т.е. на полусумму оснований.
S=60•80=4800 мм² или 48 см²
-----------------------
Чтобы использовать все данные из условия, проведем АО к продолжению ВС в сторону В.
Тогда ОС равно 80 мм, ВС=80-45=35 мм
Поскольку трапеция равнобедренная, ∆ АОВ=∆ СHD ( по равным катету и гипотенузе), и АД=80+45=125 мм
Тогда полусумма оснований (ВС+АD):2=(35+125):2=80 (мм)
Площадь, естественно, тоже будет 4800 мм²