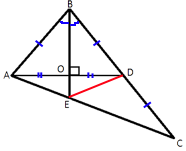
Рассмотрим треугольник ABD.
BO перпендикулярен AD (по условию задачи), т.е. ∠BOD=∠BOA=90°.
∠ABO=∠DBO (т.к. BE - биссектриса).
Получается, что треугольники ABO и DBO равны (по второму признаку равенства треугольников).
Следовательно, AB=BD.
Т.е. треугольник ABD - равнобедренный.
BO - биссектриса
этого треугольника, следовательно и медиана, и высота (по третьему свойству равнобедренного треугольника).
Следовательно, AO=OD=AD/2=104/2=52.
Проведем отрезок ED и рассмотрим треугольник BEC.
ED - медиана этого треугольника, так как делит сторону BC пополам.
Площади треугольников EDC и EDB равны (по второму свойству медианы). S EDC= S EDB=(BE*OD)/2=(104*52)/2=52*52=2704
S ABE=(BE*AO)/2=(104*52)/2=2704
Т.е. S ABE=S EDC=S EDB=2704
Тогда, S ABС=3*2704=8112
AD - медиана треугольника ABC (по условию), следовательно делит треугольник на два равных по площади треугольника ABD и ACD (по второму свойству медианы).
S ABD=(AD*BO)/2=S ABC/2
(104*BO)/2=8112/2
BO=8112/104=78
Рассмотрим треугольник ABO, он прямоугольный, тогда применим теорему Пифагора:
AB^2=BO^2+AO^2
AB^2=78^2+52^2
AB^2=6084+2704=8788
AB=√8788=√169*52=√169*13*4=2*13*√13=26√13
BC=2AB=2*26√13=52√13
Рассмотрим треугольник AOE.
OE=BE-BO=104-78=26
Так как этот треугольник тоже прямоугольный, то можно применить теорему Пифагора:
AE^2=AO^2+OE^2
AE^2=52^2+26^2=2704+676=3380
AE=√3380=√20*169=√169*5*4=13*2√5=26√5
Так как BE - биссектриса, то используя ее первое свойство запишем:
BC/AB=CE/AE
52√13/26√13=CE/(26√5)
2=CE/(26√5)
CE=52√5
AC=AE+CE=26√5+52√5=78√5
Ответ: AB=26√13, BC=52√13, AC=78√5
как то так. рисунок внизу.